Проектная работа " Логарифмы и их применение в жизни". Логарифм интерьера

Что такое логарифм

11 июля 2011

Логарифмы всегда считались сложной темой в школьном курсе математики. Существует много разных определений логарифма, но большинство учебников почему-то используют самые сложные и неудачные из них.

Мы же определим логарифм просто и наглядно. Для этого составим таблицу:

Итак, перед нами степени двойки. Если взять число из нижней строчки, то можно легко найти степень, в которую придется возвести двойку, чтобы получилось это число. Например, чтобы получить 16, надо два возвести в четвертую степень. А чтобы получить 64, надо два возвести в шестую степень. Это видно из таблицы.

А теперь — собственно, определение логарифма:

Логарифм по основанию a от аргумента x — это степень, в которую надо возвести число a, чтобы получить число x.

Обозначение: logax = b, где a — основание, x — аргумент, b — собственно, чему равен логарифм.

Например, 23 = 8 ⇒log2 8 = 3 (логарифм по основанию 2 от числа 8 равен трем, поскольку 23 = 8). С тем же успехом log2 64 = 6, поскольку 26 = 64.

Операцию нахождения логарифма числа по заданному основанию называют логарифмированием. Итак, дополним нашу таблицу новой строкой:

21	22	23	24	25	26
2	4	8	16	32	64
log2 2 = 1	log2 4 = 2	log2 8 = 3	log2 16 = 4	log2 32 = 5	log2 64 = 6

К сожалению, далеко не все логарифмы считаются так легко. Например, попробуйте найти log2 5. Числа 5 нет в таблице, но логика подсказывает, что логарифм будет лежать где-то на отрезке [2; 3]. Потому что 22 < 5 < 23, а чем больше степень двойки, тем больше получится число.

Если взять калькулятор и посчитать, чему равны такие логарифмы, то получатся очень длинные числа. Взгляните сами: log2 5 = 2,32192809... log3 8 = 1,89278926... log5 100 = 2,86135311...

Такие числа называются иррациональными: цифры после запятой можно писать до бесконечности, и они никогда не повторяются. Если логарифм получается иррациональным, его лучше так и оставить: log2 5, log3 8, log5 100.

Важно понимать, что логарифм — это выражение с двумя переменными (основание и аргумент). Многие на первых порах путают, где находится основание, а где — аргумент. Чтобы избежать досадных недоразумений, просто взгляните на картинку:

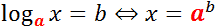
Перед нами — не что иное как определение логарифма. Вспомните: логарифм — это степень, в которую надо возвести основание, чтобы получить аргумент. Именно основание возводится в степень — на картинке оно выделено красным. Получается, что основание всегда находится внизу! Это замечательное правило я рассказываю своим ученикам на первом же занятии — и никакой путаницы не возникает.

Как считать логарифмы

С определением разобрались — осталось научиться считать логарифмы, т.е. избавляться от знака «log». Для начала отметим, что из определения следует два важных факта:

1. Аргумент и основание всегда должны быть больше нуля. Это следует из определения степени рациональным показателем, к которому сводится определение логарифма.
2. Основание должно быть отличным от единицы, поскольку единица в любой степени все равно остается единицей. Из-за этого вопрос «в какую степень надо возвести единицу, чтобы получить двойку» лишен смысла. Нет такой степени!

Такие ограничения называются областью допустимых значений (ОДЗ). Получается, что ОДЗ логарифма выглядит так: logax = b ⇒x > 0, a > 0, a ≠ 1.

Заметьте, что никаких ограничений на число b (значение логарифма) не накладывается. Например, логарифм вполне может быть отрицательным: log2 0,5 = −1, т.к. 0,5 = 2−1.

Впрочем, сейчас мы рассматриваем лишь числовые выражения, где знать ОДЗ логарифма не требуется. Все ограничения уже учтены составителями задач. Но когда пойдут логарифмические уравнения и неравенства, требования ОДЗ станут обязательными. Ведь в основании и аргументе могут стоять весьма неслабые конструкции, которые совсем необязательно соответствуют приведенным выше ограничениям.

Теперь рассмотрим общую схему вычисления логарифмов. Она состоит из трех шагов:

1. Представить основание a и аргумент x в виде степени с минимально возможным основанием, большим единицы. Попутно лучше избавиться от десятичных дробей;
2. Решить относительно переменной b уравнение: x = ab;
3. Полученное число b будет ответом.

Вот и все! Если логарифм окажется иррациональным, это будет видно уже на первом шаге. Требование, чтобы основание было больше единицы, весьма актуально: это снижает вероятность ошибки и значительно упрощает выкладки. Аналогично с десятичными дробями: если сразу перевести их в обычные, ошибок будет в разы меньше.

Посмотрим, как работает эта схема на конкретных примерах:

Задача. Вычислите логарифм: log5 25

1. Представим основание и аргумент как степень пятерки: 5 = 51; 25 = 52;

2. Составим и решим уравнение:log5 25 = b ⇒(51)b = 52 ⇒5b = 52 ⇒ b = 2;

3. Получили ответ: 2.

Задача. Вычислите логарифм:

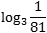
1. Представим основание и аргумент как степень тройки: 3 = 31; 1/81 = 81−1= (34)−1 = 3−4;

2. Составим и решим уравнение:

   
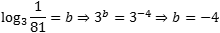
3. Получили ответ: −4.

Задача. Вычислите логарифм: log4 64

1. Представим основание и аргумент как степень двойки: 4 = 22; 64 = 26;
2. Составим и решим уравнение:log4 64 = b ⇒(22)b = 26 ⇒22b = 26 ⇒2b = 6 ⇒ b = 3;
3. Получили ответ: 3.

Задача. Вычислите логарифм: log16 1

1. Представим основание и аргумент как степень двойки: 16 = 24; 1 = 20;
2. Составим и решим уравнение:log16 1 = b ⇒(24)b = 20 ⇒24b = 20 ⇒4b = 0 ⇒ b = 0;
3. Получили ответ: 0.

Задача. Вычислите логарифм: log7 14

1. Представим основание и аргумент как степень семерки: 7 = 71; 14 в виде степени семерки не представляется, поскольку 71 < 14 < 72;
2. Из предыдущего пункта следует, что логарифм не считается;
3. Ответ — без изменений: log7 14.

Небольшое замечание к последнему примеру. Как убедиться, что число не является точной степенью другого числа? Очень просто — достаточно разложить его на простые множители. Если в разложении есть хотя бы два различных множителя, число не является точной степенью.

Задача. Выясните, являются ли точными степенями числа: 8; 48; 81; 35; 14.

8 = 2 · 2 · 2 = 23 — точная степень, т.к. множитель всего один; 48 = 6 · 8 = 3 · 2 · 2 · 2 · 2 = 3 · 24 — не является точной степенью, поскольку есть два множителя: 3 и 2; 81 = 9 · 9 = 3 · 3 · 3 · 3 = 34 — точная степень; 35 = 7 · 5 — снова не является точной степенью; 14 = 7 · 2 — опять не точная степень;

Заметим также, что сами простые числа всегда являются точными степенями самих себя.

Десятичный логарифм

Некоторые логарифмы встречаются настолько часто, что имеют специальное название и обозначение.

Десятичный логарифм от аргумента x — это логарифм по основанию 10, т.е. степень, в которую надо возвести число 10, чтобы получить число x. Обозначение: lg x.

Например, lg 10 = 1; lg 100 = 2; lg 1000 = 3 — и т.д.

Отныне, когда в учебнике встречается фраза типа «Найдите lg 0,01», знайте: это не опечатка. Это десятичный логарифм. Впрочем, если вам непривычно такое обозначение, его всегда можно переписать: lg x = log10x

Все, что верно для обычных логарифмов, верно и для десятичных.

Натуральный логарифм

Существует еще один логарифм, который имеет собственное обозначение. В некотором смысле, он даже более важен, чем десятичный. Речь идет о натуральном логарифме.

Натуральный логарифм от аргумента x — это логарифм по основанию e, т.е. степень, в которую надо возвести число e, чтобы получить число x. Обозначение: ln x.

Многие спросят: что еще за число e? Это иррациональное число, его точное значение найти и записать невозможно. Приведу лишь первые его цифры:e = 2,718281828459...

Не будем углубляться, что это за число и зачем нужно. Просто помните, что e — основание натурального логарифма: ln x = logex

Таким образом, ln e = 1; ln e2 = 2; ln e16 = 16 — и т.д. С другой стороны, ln 2 — иррациональное число. Вообще, натуральный логарифм любого рационального числа иррационален. Кроме, разумеется, единицы: ln 1 = 0.

Для натуральных логарифмов справедливы все правила, которые верны для обычных логарифмов.

Смотрите также:

1. Тест к параграфу «Что такое логарифм» (легкий)
2. Тест к уроку «Что такое логарифм» (средний)
3. Как сдать ЕГЭ по математике
4. Пробный ЕГЭ 2012 от 7 декабря. Вариант 2 (без логарифмов)
5. C2: расстояние между двумя прямыми
6. Формула простого процента: как найти исходное значение

www.berdov.com

Opoos1.ru - Авторские принты - Логарифм интерьера

Содержание и ключевые слова

Важные и популярные веб-сайты

Веб-сайт с главной страницей "Следующая Клавиша Влево" также размещает информацию на страницах В Начало, Галерея Авторского Принта и Статьи. Ниже перечислены наиболее важныe подстраницы Opoos1.ru :

# Описание URL веб-сайта

1.	Следующая клавиша влево	http://opoos1.ru
2.	В начало	http://opoos1.ru#block
3.	Галерея Авторского принта	http://opoos1.ru#block0
4.	Статьи	http://opoos1.ru#block1
5.	Объявления	http://opoos1.ru#block2
6.	Январь 13г	/thumb/EwJjaGTSa-jOyPFRXKa6jQ/580r450/943342/yanvar_13g.jpg
7.	Вечер в горах	/thumb/AEaBolD0UfUII5ST8bUqjw/580r450/943342/vecher_v_gorakh.jpg
8.	яблочный спас 98г	/thumb/kGe7gQMov_TFMVQuoAEfOg/580r450/943342/yab­lochnyy_spas_98g.jpg
9.	Чистота	/thumb/ODRgM1Nal0a6m8bRSGbgiw/580r450/943342/chisto­ta.jpg
10.	Шуршащие листики 96г	/thumb/iV2IaafxfIROkldBI5fTXw/580r450/943342/shurshashchi­ye_listi­ki_9..

Информация о Opoos1.ru из Wikipedia свободной энциклопедии:

Техническая информация

Веб-сервер Opoos1.ru расположен в Россия и используется Megagroup.ru LLC. На данном веб-сервере обслуживаются еще 16 веб-сайтов. Преобладающим языком веб-сайтов является русский.

Веб-сервер Nginx обслуживает веб-страницы Opoos1.ru. Для разметки содержания используется актуальный стандарт HTML 5. Индексация и посещение гиперссылок на веб-сайт определенно разрешаются данными робота.

Информация о сервере веб-сайта

IP-адрес:	185.32.57.148
Оператор сервера:	Megagroup.ru LLC
Количество сайтов:	17 - другие страницы с этим IP-адресом
Самые известные сайты:	Ivmrudn.com (менее известен)
Языковое распределение:	100% веб-сайтов русский

Технические характеристики к технологии сайта

ПО веб-сервера:	Nginx
Время загрузки:	0,22 секунд (быстрее, чем 88 % всех сайтов)
HTML-версия:	HTML 5
Данные робота:	all
Размер файла:	52,9 KB (615 распознанных слов в сплошном тексте)

www.webviki.ru

Проектная работа " Логарифмы и их применение в жихни"

Список использованных источников и литературы

Введение.

На протяжении 16 века быстро возрастало количество приближенных вычислений, прежде всего, в астрономии. Совершенствование инструментов, исследование планетных движений и другие работы потребовали колоссальных, иногда многолетних, расчетов. Астрономам грозила реальная опасность утонуть в невыполненных расчетах.Логарифмы были изобретены шотландским математиком Джоном Непером (1550–1617) в 1614 г. Его «Канон о логарифмах» начинался так: «Осознав, что в математике нет ничего более скучного и утомительного, чем умножение, деление, извлечение квадратных и кубических корней, и что названные операции являются бесполезной тратой времени и неиссякаемым источником неуловимых ошибок, я решил найти простое и надежное средство, чтобы избавиться от них».С точки зрения вычислительной практики, изобретение логарифмов по возможности можно смело поставить рядом с другими, более древним великим изобретением индусов – нашей десятичной системы нумерации.Через десяток лет после появления логарифмов Непера английский ученый Гунтер изобрел очень популярный прежде счетный прибор – логарифмическую линейку Она помогала астрономам и инженерам при вычислениях, она позволяла быстро получать ответ с достаточной точностью в три значащие цифры.Таким образом, потребность в сложных расчётах быстро росла. Теория логарифмов связана с именами целого ряда математиков: Генри Бригс, Эдмунд Уингейт, Уильям Отред, Н. Меркатор, Джон Спейдел, К. Бремикер, Ф. Клейн.Анализ тематики создание логарифмов достаточно актуален и представляет научный и практический интерес.Характеризуя степень научной разработанности проблематики, следует учесть, что данная тема уже анализировалась у различных авторов в различных изданиях: учебниках, монографиях, периодических изданиях и в интернете. Тем не менее, при изучении литературы и источников отмечается недостаточное количество полных и явных исследований тематики.Научная значимость данной работы состоит в оптимизации и упорядочивании существующей научно-методологической базы по исследуемой проблематике – еще одним независимым авторским исследованием. Практическая значимость темы состоит в анализе проблем как во временном, так и в пространственном разрезах.Объект исследования - «история» логарифмов.Предмет исследования – частные вопросы создание логарифмов.Цель работы – изучение темы, как с российской, так и с зарубежной точек зрения.Задача нашего исследования выяснить:

1. Как возникли логарифмы?

2. Исследовать природную сущность логарифмов.

3. Рассмотреть практическое применение логарифмов человеком.

4. В каких сферах жизнедеятельности человека применяются логарифмы?

5. Где в природе встречаются логарифмы?

История возникновения логарифма

Потребность в сложных расчётах в XVI веке быстро росла, и значительная часть трудностей была связана с умножением и делением многозначных чисел. В конце века нескольким математикам, почти одновременно, пришла в голову идея: заменить трудоёмкое умножение на простое сложение, сопоставив с помощью специальных таблиц геометрическую и арифметическую прогрессии, при этом геометрическая будет исходной. Тогда и деление автоматически заменяется на неизмеримо более простое и надёжное вычитание, а извлечение корня степени n сводится к делению логарифма подкоренного выражения на n. Первым эту идею опубликовал в своей книге «Arithmetica integra» Михаэль Штифель, который, впрочем, не

infourok.ru

opoos1.ru: Авторские принты - Логарифм интерьера

Код состояния	200
IP–адрес	185.32.57.148
Back-resolve	185.32.57.148
Content type	text/html
Кодировка	utf-8
Размер страницы	15.92 Kb.
Скорость загрузки	55.01 Kb. / s.
Общее время загрузки	0.29 −0.38 сек.
Время поиска IP	0.13 +0.02 сек.
Время подключения	0.16 +0.01 сек.
Время генерации страницы	0.16 +0.01 сек.
Начало передачи контента	0.25 −0.38 сек.
Кол–во переадресаций	0
Время переадресации	0 сек.
«Конечный» URL
Кол–во css–файлов	8
Кол–во js–файлов	15
Кол–во изображений	72
Кол–во заголовков (<h2> … <h6>)	2
Внешних ссылок	75
Внутренних ссылок	1
HTTP–сервер	nginx
Обработчик (powered–by)

domenolog.ru

Логарифмы | Все о логарифмах

Рассмотрим, как решать показательные неравенства, содержащих степени с разными основаниями. Решение таких неравенств аналогично решению соответствующих показательных уравнений.

(далее…)

Рассмотрим неравенств со степенями вида

   

   

Соответствующие показательные уравнения решаются делением либо умножением обеих частей на одну из степеней.

Поскольку степень с положительным основанием есть положительное число, деление или умножение на степень не приведёт к смене знака неравенства. Таким образом, решение таких видов неравенств со степенями аналогично решению уравнений и сводится к решению простейших показательных неравенств.

(далее…)

Примеры решения показательных неравенств продолжим рассмотрением неравенств, решаемых вынесением общего множителя за скобки.

Решение показательных неравенств этого вида тесно связано с решением соответствующих уравнений. Как и в уравнениях, в качестве общего множителя за скобки желательно выносить степень с наименьшим показателем, если основание a>1, либо наибольшим, если a<1.

(далее…)

Решение показательных неравенств продолжим рассмотрением примеров, приводимых к простейшим с использованием свойств степеней.

Решение показательных неравенств тесно связано с решением соответствующего вида показательных уравнений. Отличие — в переходе от степеней к показателям степеней. В уравнениях из равенства степеней с одинаковыми основаниями следует равенство показателей степеней, в неравенствах же знак либо не изменяется (если основание a>1), либо меняется на противоположный (при 0<a<1).

Рассмотрим решение показательных неравенствах на конкретных примерах.

   

ОДЗ: x∈R.

(далее…)

Решение простейших показательных неравенств вида

   

и

   

основывается на свойстве показательной функции

   

которая возрастает при a>1 и убывает при 0<a<1.

Рассмотрим решение простейших показательных неравенств на конкретных примерах.

   

(далее…)

Простейшие показательные неравенства — это неравенства вида

   

где a — число, a>0, a≠1.

(далее…)

Сначала выясним, как решать уравнение, в одной части которого — сумма квадратов логарифмов, а в другой — нуль.

Так как сумма неотрицательных функций равна нулю тогда и только тогда, когда каждая из функций равна нулю, сумма квадратов логарифмов равна нулю, если каждый из логарифмов равен нулю.

Поскольку логарифм единицы равен нулю, сумма квадратов логарифмов равна нулю при условии, что под знаком каждого из логарифмов стоит единица:

   

(далее…)

www.logarifmy.ru

Логарифмы

Логарифмы изучаются в старших классах и считаются достаточно сложными для понимания. На самом же деле, ничего сложного здесь нет — надо только начать изучение.

По существу, нахождение логарифма — это операция, обратная возведению в степень. Отсюда возникают все свойства и ограничения логарифма.

Логарифмические функции часто попадаются на экзаменах в виде уравнений и неравенств. Поэтому умение работать с логарифмами и твердое знание их свойств совершенно необходимы.

Глава 1. Понятие логарифма § 1. Что такое логарифм § 2. Тест к параграфу «Что такое логарифм» (легкий) § 3. Тест к уроку «Что такое логарифм» (средний) § 4. Тест к уроку «Что такое логарифм» (тяжелый) § 5. Основные свойства логарифмов Глава 2. Логарифмические уравнения § 1. Простейшие логарифмические уравнения — первые шаги § 2. Логарифмические уравнения: комплект видеоуроков для изучения § 3. Уравнения, квадратные относительно логарифма, и другие нестандартные ситуации § 4. Решение логарифмических уравнений — заключительный комплект видеоуроков Глава 3. Логарифмические неравенства § 1. Преобразование логарифмических неравенств с одинаковым основанием § 2. Логарифмические неравенства с переменным основанием § 3. Логарифмические неравенства, сводящиеся к квадратным § 4. Неравенства, квадратные относительно логарифма § 5. Дробно-рациональные неравенства с логарифмами § 6. Сложные логарифмические неравенства Глава 4. Что такое логарифм Глава 5. Свойства логарифмов Глава 6. Логарифмические выражения Глава 7. Логарифмическая функция § 10. Логарифм с переменным основанием и метод рационализации § 18. Решение сложных логарифмических неравенств разными способами § 19. Совмещение метода рационализации и метода интервалов § 20. Подробное решение логарифмического неравенства методом рационализации § 21. Метод рационализации логарифмических неравенств 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267

www.berdov.com

Логарифм | Наука | FANDOM powered by Wikia

Рис. 1. Графики логарифмических функций

Логарифм числа $ b $ по основанию $ a $ определяется как показатель степени, в которую надо возвести число a, чтобы получить число b. Обозначение: $ \log_a b $. Из определения следует, что записи $ \log_a b = x $ и $ a^x=b $ эквивалентны.

Пример: $ \log_2 8 = 3 $, потому что $ 2^3 = 8 $.

Вещественный логарифм Править

Логарифм вещественного числа $ \log_a b $ имеет смысл при $ a>0, a \ne 1, b>0 $.

Наиболее широкое применение нашли следующие виды логарифмов.

• Десятичные: $ \lg\,a $, основание: число 10.
• Натуральные: $ \ln\,a $, основание: e (число Эйлера).
• Двоичные: $ \log_2\,a $ или $ \operatorname{lb}\,a $, основание: число 2. Они применяются в теории информации и информатике.

Свойства Править

• Основное логарифмическое тождество: $ a^{\log_a b} = b $
• $ \log_a a = 1;\;\log_a 1 = 0 $
• $ \log_a (bc) = \log_a b + \log_a c $
• $ \log_a \frac{b}{c} = \log_a b - \log_a c $
• $ \log_a (b^p) = p\ \log_a b $
• $ \log_a \sqrt[c] {b} = \frac{1}{c} \log_a b $
• $ {\log_{a^q}{b}}^p = \frac{p}{q}\log_a{b} $
• $ \log_{a^k} b^k = \log_a b $
• $ \log_a b = \frac{\log_c b }{\log_c a} $ (замена основания логарифма)
• $ \log_a b = \frac {1}{\log_b a} $
• $ a^{log_c d}=d^{log_c a} $

Натуральные логарифмы Править

Для производной натурального логарифма справедлива простая формула:

$ (\ln x )' = \frac{1}{x} $

По этой причине в математических исследованиях преимущественно используют именно натуральные логарифмы. Они нередко появляются при решении дифференциальных уравнений, исследовании статистических зависимостей (например, распределения простых чисел) и т. п.

При $ -1 < x \leqslant 1 $ справедливо равенство нплшпдп В частности, нплшпдп Формула (1) не имеет большой практической ценности из-за того, что ряд очень медленно сходится, и значение $ x $ ограничено весьма узким диапазоном. Однако нетрудно получить из неё более удобную формулу: нплшпдп Этот ряд сходится быстрее, а кроме того, левая часть формулы теперь может выразить логарифм любого положительного числа.

Связь с десятичным логарифмом: $ \ln x = 2{,}30259\ \lg x;\ \ \lg x = 0{,}43429\ \ln x $.

Десятичные логарифмы Править

Рис. 2. Логарифмическая шкала

Логарифмы по основанию 10 (обозначение: lg a) до изобретения калькуляторов широко применялись для вычислений. Неравномерная шкала десятичных логарифмов обычно наносится и на логарифмические линейки. Подобная шкала широко используется в различных областях науки, например:

Комплексный логарифм Править

Рис. 3. Комплексный логарифм (мнимая часть)

Для комплексных чисел логарифм определяется так же, как вещественный. Начнём с натурального логарифма, который тоже обозначим $ ~\ln w~ $ и определим как комплексное число $ z $ такое, что $ e^z=w $. Комплексный логарифм существует для любого $ w \ne 0 $, и его вещественная часть определяется однозначно, в то время как мнимая имеет бесконечное множество значений. Если представить $ w $ в показательной форме:

$ w=r \cdot e^{i \varphi} $,

то логарифм $ \ln~w $ находится по формуле:

$ \ln w = \ln r + i \left ( \varphi + 2 \pi k \right ) \ . $

Здесь $ \ln~r $ — вещественный логарифм, $ r=|w| $, $ k $ — произвольное целое число. Значение, получаемое при $ k=0 $, называется главным значением комплексного натурального логарифма; принято брать в нём значение аргумента $ \varphi $ в интервале $ (-\pi, \pi] $.

Из формулы следует:

• Вещественная часть логарифма определяется по формуле:
$ \operatorname{Re}(\ln(x+iy)) = \frac{1}{2} \ln(x^2+y^2) $
• Логарифм отрицательного числа находится по формуле:
$ \ln (-x) = \ln x + i \pi (2 k + 1) \qquad (x>0,\ k = 0, \pm 1, \pm 2 \dots) $

Примеры (приведено главное значение логарифма):

• $ \ln (-1) = i \pi $
• $ \ln (i) = i \frac{\pi} {2} $
• $ \ln (-i) = -i \frac{\pi} {2} $

Аналогично рассматриваются комплексные логарифмы с другим основанием. Следует, однако, быть осторожным при преобразованиях комплексных логарифмов, принимая во внимание, что они многозначны, и поэтому из равенства логарифмов каких-либо выражений не следует равенство этих выражений. Пример ошибочного рассуждения:

$ i\pi = \ln(-1) = \ln((-i)^2) = 2\ln(-i) = 2(-i\pi/2) = -i\pi $ — явная нелепость.

Отметим, что слева стоит главное значение логарифма, а справа — значение из нижележащей ветви ($ k=-1 $). Причина ошибки — неосторожное использования свойства $ \log_a{(b^p)} = p~\log_a b $, которое, вообще говоря, подразумевает в комплексном случае весь бесконечный набор значений логарифма, а не только главное значение.

Логарифмическая функция Править

Комплексная логарифмическая функция — пример римановой поверхности; её мнимая часть (рис. 3) состоит из бесконечного числа ветвей, закрученных наподобие спирали. Эта поверхность односвязна; её единственный нуль (первого порядка) получается при $ z=1 $, особые точки: $ z=0 $ и $ z=\infty $ (точки разветвления бесконечного порядка).

Исторический очерк Править

Вещественный логарифм Править

Потребность в сложных расчётах в XVI веке быстро росла, и значительная часть трудностей была связана с умножением и делением многозначных чисел. В конце века нескольким математикам, почти одновременно, пришла в голову идея: заменить трудоёмкое умножение на простое сложение, сопоставив с помощью специальных таблиц геометрическую и арифметическую прогрессии, при этом геометрическая будет исходной. Тогда и деление автоматически заменяется на неизмеримо более простое и надёжное вычитание. Первым эту идею опубликовал в своей книге «Arithmetica integra» Михаэль Штифель, который, впрочем, не приложил серьёзных усилий для реализации своей идеи.

В 1614 году шотландский математик-любитель Джон Непер опубликовал на латинском языке сочинение под названием «Описание удивительной таблицы логарифмов». В нём было краткое описание логарифмов и их свойств, а также 8-значные таблицы логарифмов синусов, косинусов и тангенсов, с шагом 1'. Термин логарифм, предложенный Непером, утвердился в науке.

Понятия функции тогда ещё не было, и Непер определил логарифм кинематически, сопоставив равномерное и логарифмически-замедленное движение. В современной записи модель Непера можно изобразить дифференциальным уравнением: dx/x = -dy/M, где M — масштабный множитель, введенный для того, чтобы значение получилось целым числом с нужным количеством знаков (десятичные дроби тогда ещё не нашли широкого применения). Непер взял M = 10000000.

Строго говоря, Непер табулировал не ту функцию, которая сейчас называется логарифмом. Если обозначить его функцию LogNap(x), то она связана с натуральным логарифмом следующим образом:

$ \operatorname{LogNap}(x) = M * (\ln(M) - \ln(x)) $

Очевидно, LogNap(M) = 0, то есть логарифм «полного синуса» есть нуль — этого и добивался Непер своим определением. LogNap(0) = ∞.

Основное свойство логарифма Непера: если величины образуют геометрическую прогрессию, то их логарифмы образуют прогрессию арифметическую. Однако правила логарифмирования для неперовой функции отличались от правил для современного логарифма.

Например, LogNap(ab) = LogNap(a) + LogNap(b) — LogNap(1).

К сожалению, все значения таблицы Непера содержали вычислительную ошибку после шестого знака. Однако это не помешало новой методике вычислений получить широчайшую популярность, и составлением логарифмических таблиц занялись многие европейские математики, включая Кеплера.

В 1620-е годы Эдмунд Уингейт и Уильям Отред изобрели первую логарифмическую линейку, до появления карманных калькуляторов — незаменимый инструмент инженера.

Близкое к современному понимание логарифмирования — как операции, обратной возведению в степень — впервые появилось у Валлиса и Иоганна Бернулли, а окончательно было узаконено Эйлером в XVIII веке. В книге «Введение в анализ бесконечных» (1748) Эйлер дал современные определения как показательной, так и логарифмической функций, привёл разложение их в степенные ряды, особо отметил роль натурального логарифма.

Эйлеру принадлежит и заслуга распространения логарифмической функции на комплексную область.

Комплексный логарифм Править

Первые попытки распространить логарифмы на комплексные числа предпринимали на рубеже XVII—XVIII веков Лейбниц и Иоганн Бернулли, однако создать целостную теорию им не удалось — в первую очередь по той причине, что тогда ещё не было ясно определено само понятие логарифма. Дискуссия по этому поводу велась сначала между Лейбницем и Бернулли, а в середине XVIII века — между Даламбером и Эйлером. Бернулли и Даламбер считали, что следует определить log(-x) = log(x). Полная теория логарифмов отрицательных и комплексных чисел была опубликована Эйлером в 1747—1751 годах и по существу ничем не отличается от современной.

Хотя спор продолжался (Даламбер отстаивал свою точку зрения и подробно аргументировал её в статье своей «Энциклопедии» и в других трудах), однако точка зрения Эйлера быстро получила всеобщее признание.

Логарифмические таблицы Править

Логарифмические таблицы

Из свойств логарифма следует, что вместо трудоёмкого умножения многозначных чисел достаточно найти (по таблицам) и сложить их логарифмы, а потом по тем же таблицам выполнить потенцирование, то есть найти значение результата по его логарифму. Выполнение деления отличается только тем, что логарифмы вычитаются. Лаплас говорил, что изобретение логарифмов «продлило жизнь астрономов», многократно ускорив процесс вычислений.

При переносе десятичной запятой в числе на $ n $ разрядов значение десятичного логарифма этого числа изменяется на $ n $. Например, $ \lg 8314{,}63 = \lg 8{,}31463 + 3 $. Отсюда следует, что достаточно составить таблицу десятичных логарифмов для чисел в диапазоне от 1 до 10.

Первые таблицы логарифмов опубликовал Джон Непер (1614), и они содержали только логарифмы тригонометрических функций, причём с ошибками. Независимо от него свои таблицы опубликовал Иост Бюрги, друг Кеплера (1620). В 1617 году оксфордский профессор математики Генри Бригс опубликовал таблицы, которые уже включали десятичные логарифмы самих чисел, от 1 до 1000, с 8 (позже — с 14) знаками. Но и в таблицах Бригса обнаружились ошибки. Первое безошибочное издание на основе таблиц Вега (1783) появилось только в 1857 году в Берлине (таблицы Бремивера).

В России первые таблицы логарифмов были изданы в 1703 году при участии Л. Ф. Магницкого. В СССР выпускались несколько сборников таблиц логарифмов.

• Брадис В. М. Четырехзначные математические таблицы. 44-е издание, М., 1973.

Таблицы Брадиса (1921) использовались в учебных заведениях и в инженерных расчётах, не требующих большой точности. Они содержали мантиссы десятичных логарифмов чисел и тригонометрических функций, натуральные логарифмы и некоторые другие полезные расчётные инструменты.

• Вега Г. Таблицы семизначных логарифмов, 4-е издание, М., 1971.

Профессиональный сборник для точных вычислений.

• Пятизначные таблицы натуральных значений тригонометрических величин, их логарифмов и логарифмов чисел, 6 изд., М.: Наука, 1972.
• Таблицы натуральных логарифмов, 2-е издание, в 2 томах, М.: Наука, 1971.

bg:Логаритъм bs:Logaritam ca:Logaritme cs:Logaritmus da:Logaritme de:Logarithmus el:Λογάριθμος en:Logarithm eo:Logaritmo es:Logaritmo fa:لگاریتم fi:Logaritmi fr:Logarithme gl:Función logaritmo he:לוגריתם hi:लघुगणक hr:Logaritam hu:Logaritmus ia:Logarithmo id:Logaritma io:Logaritmo is:Logri it:Logaritmo ja:対数 ko:로그 la:Logarithmus lt:Logaritmas lv:Logaritms ml:ലോഗരിതം ms:Logaritma nl:Logaritme no:Logaritme pl:Logarytm pt:Logaritmo ro:Logaritm scn:Lugarìttimu simple:Logarithm sk:Logaritmus sl:Logaritem sr:Логаритам sv:Logaritm th:ลอการิทึม tr:Logaritma uk:Логарифм zh:对数

ru.science.wikia.com

---

• 
  Штольца интерьер
• 
  Интерьер химитек
• 
  Интерьер полуторки
• 
  Интерьер булочной
• 
  Грани интерьера
• 
  Интерьер макдональдса
• 
  Интерьер спортзал
• 
  Бионика интерьер
• 
  Рождественские интерьеры
• 
  Пазлы интерьеров
• 
  Бабушкин интерьер